Overview

Problem: Traditional kitting systems often use few pre-defined kits that do not adapt to variability such as part shortages or unexpected delays in real time. This inflexibility can lead to inefficiencies, higher cognitive load for workers, and longer production times.

Solution: We propose a dynamic robotic kitting planner that segments and schedules assembly tasks to minimize idle time and reduce makespan. Using a bilevel optimization framework, the upper-level optimization determines the task segmentation to minimize idle time and the lower-level optimization designs the physical layout of parts on the kitting tray to ensure usability and logical grouping.

What is Kitting?

Kitting is the process of preparing and grouping the required components for assembly of a given product. Kitting is advantageous for assemblies involving numerous small components and products that support a wide range of customizations. For example, it is used in electronics and automobile manufacturing (https://tulip.co/blog/the-kitting-process-for-manufacturers/).

Problem Setup

We have a set of tasks to finish represented by a Directed Acyclic Graph (DAG). An edge between two tasks a -> b indicates that task a has to be finished before task b can begin. The tasks that the human can do depends on the assembly parts that the robot delivers on the kitting tray. The robot has estimates of how long it takes the human to perform each task and the availability of parts. How does the robot determine what parts to place on the kitting tray at any given time in order to maximize team throughput?

Approach

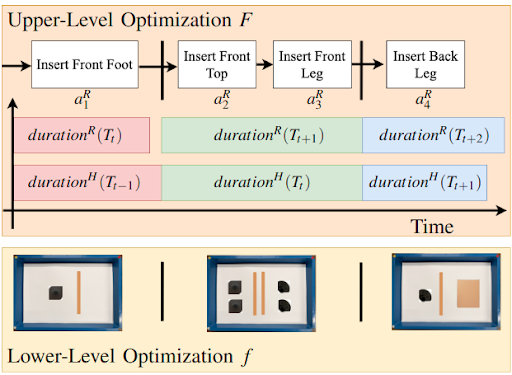
Bilevel Optimization

The upper level problem optimizes for an objective function that depends on the outcome of the lower level problem. In the upper level problem, the robot segments the task such that human idle time is minimized. The first segment is the kit that the robot delivers in the next time step. The “goodness” of the segmentation is influenced by the lower level problem of how well the assembly parts fit in the kit. For more details, please refer to the paper.

Experiments

User Study

In the user study, articipants assembled a miniature table that required connecting four legs, connectors and a flat surface plank by snapping the pieces together and securing with screws and nuts. The robot has to deliver four legs, eight connectors, small/large screw and nuts boxes on the kitting tray.


Our optimization produced the following kitting strategy based on an initial data set of human task times.


The first kit allows the human to connect a leg to a top connector. The third kit is repeated until the task is done. Here we do not consider part shortages. In the simulation experiment, we model various assembly part arrival time distributions and part-feeding machine breakdown conditions (i.e. the part is not available to the robot until after the machine is repaired.)

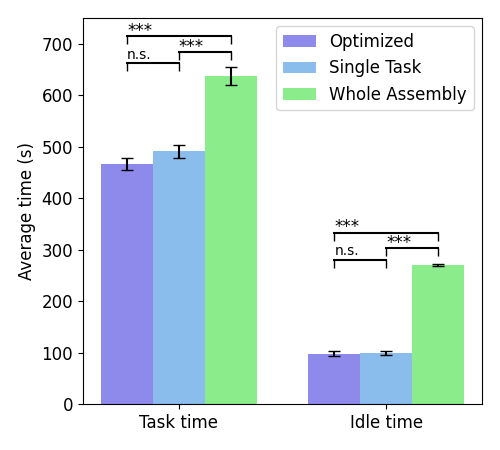
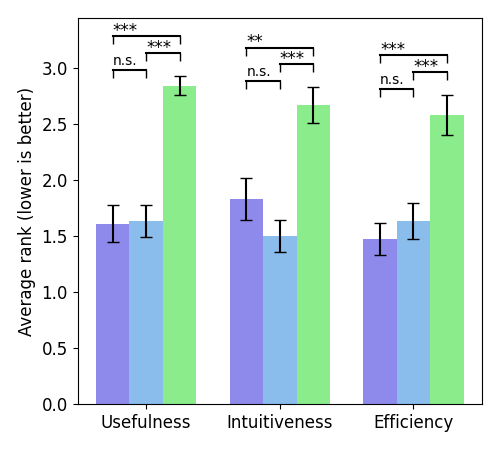
The baselines that we compare to are Single Task where the robot delivers parts for a single task at a time and Whole Assembly where all the parts are delivered at once. Our approach Optimized has a shorter total task time and idle times than Whole Assembly and is also rated more useful and efficient.

Discrete Event Simulation

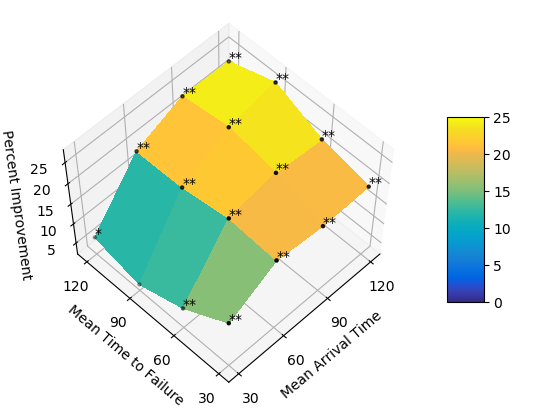
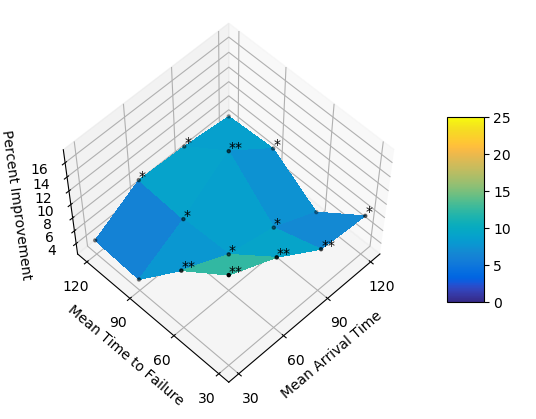
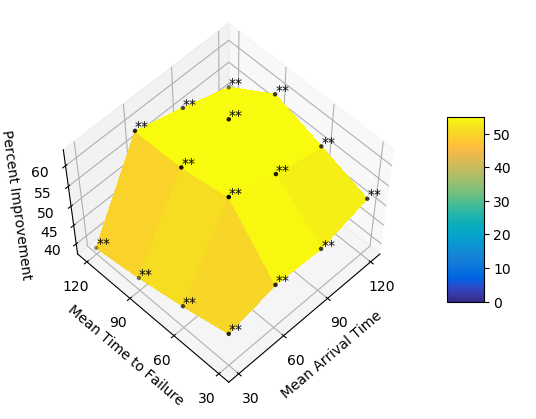
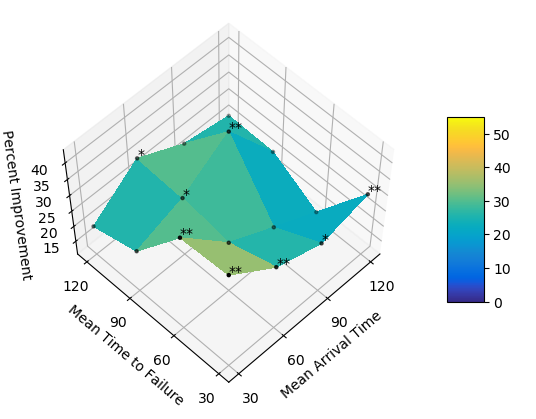
We model the arrival of assembly parts as a Poisson process with rate \(1/MAT\) where \(MAT\) is the mean arrival time. The machine breakdown is modeled similarly with the mean time to failure denoted by \(MTTF\). The figures below are the percent improvement in total task time of Optimized over Whole Assembly (top-left) and over Single Task (top-right), and the percent improvement in human idle time of Optimized over Whole Assembly (bottom-left) and over Single Task (bottom-right). The total task time and human idle time are significantly shorter for Optimized than the baselines. Optimized is most advantageous over Whole Assembly when there is high part shortage (\(MAT\) is high). Optimized is most advantageous over Single Task when there are many machine failures (\(MTTF\) is low).